Lecture 08: Multivariate Analysis

Multivariate Correlation Model

Jihong Zhang*, Ph.D

Educational Statistics and Research Methods (ESRM) Program*

University of Arkansas

2024-10-09

Outline

Today's Class

• Multivariate linear models: An introduction
• How to form multivariate models in lavaan
• What parameters mean
• How they relate to the multivariate normal distribution

Multivariate Models: An Introduction

Multivariate Linear Models

• The next set of lectures are provided to give an overview of multivariate linear models
  • Models for more than one dependent/outcome variables
• Our focus today will be on models where the DV is plausibly continuous
  • so we’ll use error terms that are multivariate normally distributed
  • Not a necessity – generalized multivariate models are possible

Classical vs. Contemporary Methods

• In “classical” multivariate textbooks and classes multivariate linear models fall under the names of Multivariate ANOVA (MANOVA) and Multivariate Regression

• These methods rely upon least squares estimation which:

  1. Inadequate with missing data
  2. Offers very limited methods of setting covariance matrix structures
  3. Does not allow for different sets predictor variables for each outcome
  4. Does not give much information about model fit
  5. Does not provide adequate model comparison procedures

• The classical methods have been subsumed into the modern (likelihood or Bayes-based) multivariate methods

  • Subsume: include or absorb (something) in something else
  • Meaning: modern methods do what classical methods do (and more)

Contemporary Methods for Estimating Multivariate Linear Models

• We will discuss three large classes of multivariate linear modeling methods:

  • Path analysis models (typically through structural equation modeling and path analysis software)
  • Linear mixed models (typically through linear models software)
  • Psychological network models (typically through psychological network software)
  • Bayesian networks (frequently not mentioned in social sciences but subsume all we are doing)

• The theory behind each is identical – the main difference is in software

  • Some software does a lot (Mplus software is likely the most complete), but none (as of 2024) do it all

• We will start with path analysis (via the lavaan package) as the modeling method is more direct but then move to linear mixed models software (via the nlme and lme4 packages)

• Bayesian networks will be discussed in the Bayes section of the course and will use entirely different software

The “Curse” of Dimensionality: Shared Across Models

• Having lots of parameters creates a number of problems

  • Estimation issues for small sample sizes
  • Power to detect effects
  • Model fit issues for large numbers of outcomes

• Curse of dimensionality: for multivariate normal data, there’s a quadratic increase in the number of parameters as the number of outcomes increases linearly

• To be used as an analysis model, however, a model-implied covariance structure must “fit” as well as the saturated/unstructured covariance matrix

  \[ S \rightarrow \Sigma \]

Biggest Difference From Univariate Models: Model Fit

1. In univariate linear models, the “model for the variance” wasn’t much of a model - There was one variance term possible (\(\sigma^2_e\)) and one term estimated
   • A saturated model - all variances/covariances are freely estimated without any constrains - Model fit was always perfect
2. In multivariate linear models, because of the number of variances/covariances, oftentimes models are not saturated for the variances
   • Therefore, model fit becomes an issue
3. Any non-saturated model for the variances must be shown to fit the data before being used for interpretation
   • “fit the data” has differing standards depending on software type used.

Today’s Example Data

• Data are simulated based on the results reported in:

• Sample of 350 undergraduates (229 women, 121 men)

  • In simulation, 10% of variables were missing (using missing completely at random mechanism).

Dictionary

1. Prior Experience at High School Level (HSL)
2. Prior Experience at College Level (CC)
3. Perceived Usefulness of Mathematics (USE)
4. Math Self-Concept (MSC)
5. Math Anxiety (MAS)
6. Math Self-Efficacy (MSE)
7. Math Performance (PERF)
8. Female (sex variable: 0 = male; 1 = female)

library(ESRM64503)
library(kableExtra)
library(tidyverse)
library(DescTools) # Desc() allows you to quick screen data
options(digits=3)
head(dataMath)

  id hsl cc use msc mas mse perf female
1  1  NA  9  44  55  39  NA   14      1
2  2   3  2  77  70  42  71   12      0
3  3  NA 12  64  52  31  NA   NA      1
4  4   6 20  71  65  39  84   19      0
5  5   2 15  48  19   2  60   12      0
6  6  NA 15  61  62  42  87   18      0

dim(dataMath)

[1] 350   9

Desc(dataMath[,2:8], plotit = FALSE, conf.level = FALSE)

────────────────────────────────────────────────────────────────────────────── 
Describe dataMath[, 2:8] (data.frame):

data frame: 350 obs. of  7 variables
        145 complete cases (41.4%)

  Nr  Class  ColName  NAs         Levels
  1   int    hsl      36 (10.3%)        
  2   int    cc       37 (10.6%)        
  3   int    use      24 (6.9%)         
  4   int    msc      39 (11.1%)        
  5   int    mas      46 (13.1%)        
  6   int    mse      34 (9.7%)         
  7   int    perf     60 (17.1%)        


────────────────────────────────────────────────────────────────────────────── 
1 - hsl (integer)

  length      n    NAs  unique    0s   mean  meanCI'
     350    314     36       8     0   4.92    4.92
          89.7%  10.3%          0.0%           4.92
                                                   
     .05    .10    .25  median   .75    .90     .95
    3.00   3.00   4.00    5.00  6.00   6.00    7.00
                                                   
   range     sd  vcoef     mad   IQR   skew    kurt
    7.00   1.32   0.27    1.48  2.00  -0.26   -0.41
                                                   

   value  freq   perc  cumfreq  cumperc
1      1     1   0.3%        1     0.3%
2      2    11   3.5%       12     3.8%
3      3    34  10.8%       46    14.6%
4      4    71  22.6%      117    37.3%
5      5    79  25.2%      196    62.4%
6      6    88  28.0%      284    90.4%
7      7    27   8.6%      311    99.0%
8      8     3   1.0%      314   100.0%

' 0%-CI (classic)

────────────────────────────────────────────────────────────────────────────── 
2 - cc (integer)

  length      n    NAs  unique     0s   mean  meanCI'
     350    313     37      28     21  10.31   10.31
          89.4%  10.6%           6.0%          10.31
                                                    
     .05    .10    .25  median    .75    .90     .95
    0.00   2.00   6.00   10.00  14.00  19.00   20.00
                                                    
   range     sd  vcoef     mad    IQR   skew    kurt
   27.00   5.89   0.57    5.93   8.00   0.17   -0.43
                                                    
lowest : 0 (21), 1 (5), 2 (9), 3 (9), 4 (12)
highest: 23, 24, 25, 26, 27

heap(?): remarkable frequency (8.6%) for the mode(s) (= 10, 13)

' 0%-CI (classic)

────────────────────────────────────────────────────────────────────────────── 
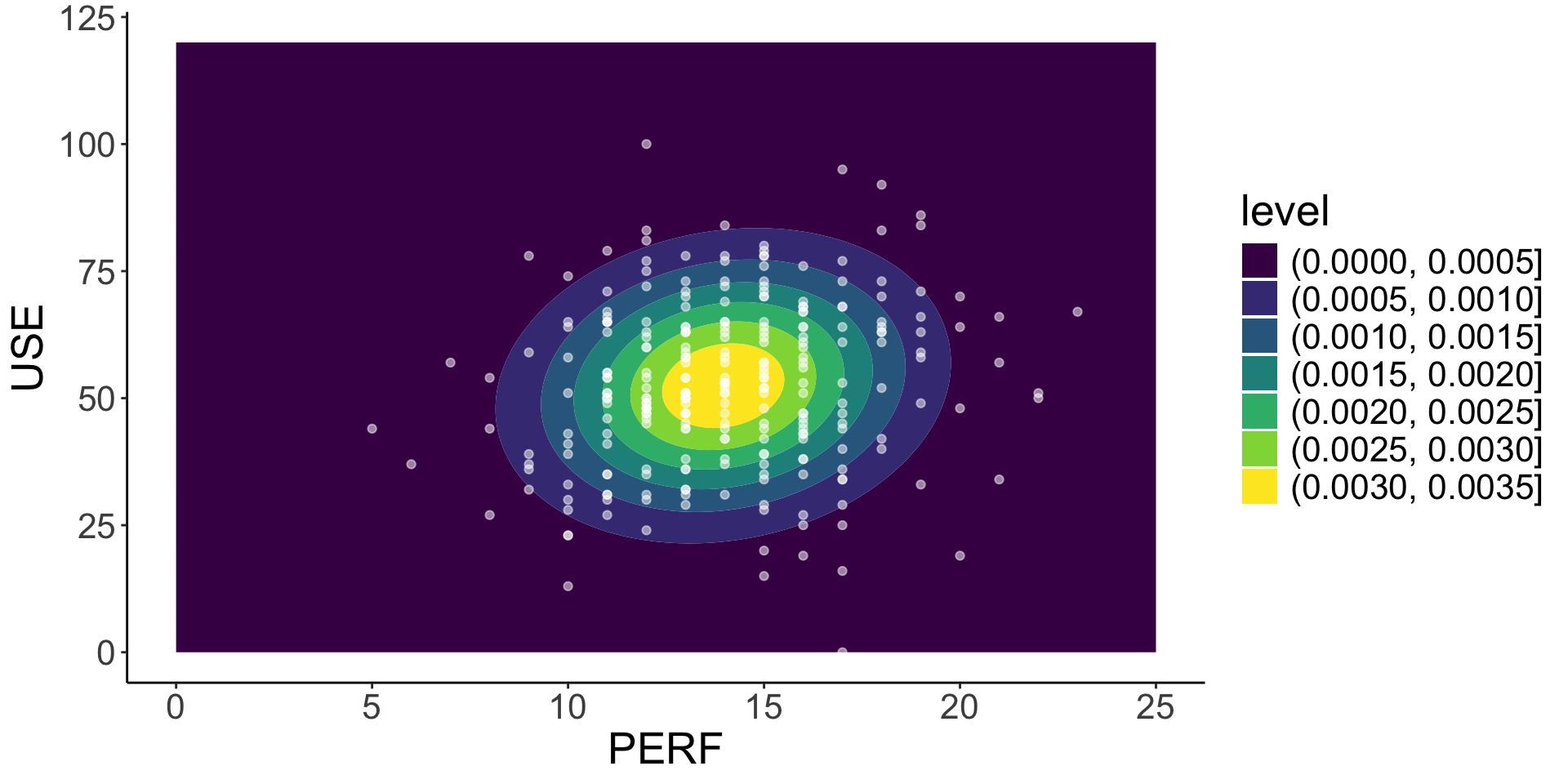
3 - use (integer)

  length      n    NAs  unique     0s   mean  meanCI'
     350    326     24      71      1  52.50   52.50
          93.1%   6.9%           0.3%          52.50
                                                    
     .05    .10    .25  median    .75    .90     .95
   25.50  31.00  42.25   52.00  64.00  71.50   77.75
                                                    
   range     sd  vcoef     mad    IQR   skew    kurt
  100.00  15.81   0.30   16.31  21.75  -0.11   -0.08
                                                    
lowest : 0, 13, 15, 16, 19 (2)
highest: 84 (2), 86, 92, 95, 100

' 0%-CI (classic)

────────────────────────────────────────────────────────────────────────────── 
4 - msc (integer)

  length      n    NAs  unique     0s   mean  meanCI'
     350    311     39      76      0  49.79   49.79
          88.9%  11.1%           0.0%          49.79
                                                    
     .05    .10    .25  median    .75    .90     .95
   24.00  29.00  38.00   49.00  61.00  72.00   80.50
                                                    
   range     sd  vcoef     mad    IQR   skew    kurt
   98.00  16.96   0.34   16.31  23.00   0.23   -0.09
                                                    
lowest : 5, 9, 12, 15, 16 (2)
highest: 87 (3), 89, 91, 94, 103

' 0%-CI (classic)

────────────────────────────────────────────────────────────────────────────── 
5 - mas (integer)

  length      n    NAs  unique     0s   mean  meanCI'
     350    304     46      57      1  31.50   31.50
          86.9%  13.1%           0.3%          31.50
                                                    
     .05    .10    .25  median    .75    .90     .95
   13.00  17.00  24.75   32.00  39.00  45.70   50.00
                                                    
   range     sd  vcoef     mad    IQR   skew    kurt
   62.00  11.32   0.36   10.38  14.25  -0.13   -0.17
                                                    
lowest : 0, 2, 3 (2), 5, 6
highest: 54 (2), 55 (2), 56, 58, 62

' 0%-CI (classic)

────────────────────────────────────────────────────────────────────────────── 
6 - mse (integer)

  length      n    NAs  unique     0s   mean  meanCI'
     350    316     34      56      0  73.41   73.41
          90.3%   9.7%           0.0%          73.41
                                                    
     .05    .10    .25  median    .75    .90     .95
   54.00  58.00  65.00   73.00  81.00  88.50   92.25
                                                    
   range     sd  vcoef     mad    IQR   skew    kurt
   60.00  11.89   0.16   11.86  16.00   0.06   -0.26
                                                    
lowest : 45 (2), 46, 47, 49 (2), 50 (4)
highest: 98, 100, 101 (2), 103, 105 (2)

' 0%-CI (classic)

────────────────────────────────────────────────────────────────────────────── 
7 - perf (integer)

  length      n    NAs  unique     0s   mean  meanCI'
     350    290     60      19      0  13.97   13.97
          82.9%  17.1%           0.0%          13.97
                                                    
     .05    .10    .25  median    .75    .90     .95
    9.45  10.00  12.00   14.00  16.00  18.00   19.00
                                                    
   range     sd  vcoef     mad    IQR   skew    kurt
   18.00   2.96   0.21    2.97   4.00   0.16    0.14
                                                    
lowest : 5, 6, 7 (2), 8 (3), 9 (8)
highest: 19 (10), 20 (4), 21 (3), 22 (2), 23

heap(?): remarkable frequency (13.8%) for the mode(s) (= 13)

' 0%-CI (classic)

Using MVN Likelihoods in lavaan

The lavaan package is developed by Dr. Yves Rosseel to provide useRs, researchers and teachers a free open-source, but commercial-quality package for latent variable modeling. You can use lavaan to estimate a large variety of multivariate statistical models, including path analysis, confirmatory factor analysis, structural equation modeling and growth curve models.

• lavaan’s default model is a linear (mixed) model that uses ML with the multivariate normal distribution

• ML is sometimes called a full information method (FIML)

  • Full information is the term used when each observation gets used in a likelihood function
  • The contrast is limited information (not all observations used; typically summary statistics are used)

install.packages('lavaan')
library(lavaan)

Revisiting Univariate Linear Regression

• We will begin our discussion by starting with perhaps the simplest model we will see: a univariate empty model
  • We will use the PERF variable from our example data: Performance on a mathematics assessment
• The empty model for PERF is:
  • \(e_{i, PERF} \sim N(0, \sigma^2_{e,PERF})\)
  • Two parameters are estimated: \(\beta_{0,PERF}\) and \(\sigma^2_{e,PERF}\)

\[ \text{PERF}_i = \beta_{0,\color{tomato}{PERF}} + e_{i, \color{tomato}{PERF}} \]

• Here, the additional subscript is added to denote these terms are part of the model for the PERF variable
  • We will need these when we get to multivariate models and path analysis

lavaan Syntax: General

• Estimating a multivariate model using lavaan contains three steps:
  1. Build a string object including syntax for models (e.g., model01.syntax)
  2. Estimate the model with observed data and save it to a fit object(e.g., model01.fit <- cfa(mode01.syntax, data))
  3. Extract the results from the fit object
• The lavaan package works by taking the typical R model syntax (as from lm()) and putting it into a quoted character variable
  • lavaan model syntax also includes other commands used to access other parts of the model (really, parts of the MVN distribution)

• Here are rules of lavaan model syntax:
  • ~~ indicates variance or covariance between variables on either side (perf ~~ perf) estimates variance
  • ~1 indicates intercept for one variable (perf~1)
  • ~ indicates LHS regresses on RHS (perf~use)

## Syntax for model01
1model01.syntax <- "
## Variances:
perf ~~ perf

## Means:
perf ~ 1
"
## Estimation for model01
2model01.fit <- cfa(model01.syntax, data=dataMath, mimic="MPLUS", fixed.x = TRUE, estimator = "MLR")

## Print output
summary(model01.fit)

1

model syntax is a string object containing our model specification

2

We use the cfa() function to run the model based on the syntax

lavaan 0.6-19 ended normally after 8 iterations

  Estimator                                         ML
  Optimization method                           NLMINB
  Number of model parameters                         2

                                                  Used       Total
  Number of observations                           290         350
  Number of missing patterns                         1            

Model Test User Model:
                                              Standard      Scaled
  Test Statistic                                 0.000       0.000
  Degrees of freedom                                 0           0

Parameter Estimates:

  Standard errors                             Sandwich
  Information bread                           Observed
  Observed information based on                Hessian

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)
    perf             13.966    0.174   80.397    0.000

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)
    perf              8.751    0.756   11.581    0.000

Model Parameter Estimates and Assumptions

Summary of lavaan's cfa()

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)
    perf             13.966    0.174   80.397    0.000
Variances:
                   Estimate  Std.Err  z-value  P(>|z|)
    perf              8.751    0.756   11.581    0.000

• Parameter Estimates:
  • \(\beta_{0,PERF} = 13.966\)
  • \(\sigma^2_{e,PERF} = 8.751\)
• Using the model estimates, we known that:

\[ \text{PERF}_i \sim N(13.966, 8.751) \]

Multivariate Correlation Models

Model 2: Adding One More Variable to the Model

• Variables: We already know how to use lavaan to estimate univariate model, let’s move on to model two variables as outcomes

  • Mathematics performance (perf)
  • Perceived Usefulness of Mathematics (use)

• Assumption: We will assume both to be continuous variables (conditionally MVN)

• Research Question: Whether or not students’ performance are significantly related to their perceived usefulness of mathematics?

• Initially, we will only look at an empty model with these two variables:

  • Empty models are baseline models
  • We will use these to show how such models look based on the characteristics of the multivariate normal distribution
  • We will also show the bigger picture when modeling multivariate data: how we must be sure to model the covariance matrix correctly

Multivariate Empty Model: The Notation

• The multivariate model for perf and use is given by two regression models, which are estimated simultaneously:

\[ \text{PERF}_i = \beta_{0,\text{PERF}}+e_{i,\text{PERF}} \]

\[ \text{USE}_i = \beta_{0,\text{USE}}+e_{i,\text{USE}} \]

• As there are two variables, the error terms have a joint distribution that will be multivariate normal

\[ \begin{bmatrix}e_{i,\text{PERF}}\\e_{i,\text{USE}}\end{bmatrix} \sim \mathbf{N}_2 (\mathbf{0}=\begin{bmatrix}0\\0\end{bmatrix}, \mathbf{R}=\begin{bmatrix}\sigma^2_{e,\text{PERF}} & \sigma_{e,\text{PERF},\text{USE}}\\ \sigma_{e,\text{PERF},\text{USE}}&\sigma^2_{e,\text{USE}}\end{bmatrix}) \]

• Each error term (diagonal elements in \(\mathbf{R}\)) has its own variance but now there is a covariance between error terms
  • We will soon that the overall \(\mathbf{R}\) matrix structure can be modified

Data Model

• Before showing the syntax and the results, we must first describe how the multivariate empty model implies how our data should look

• Multivariate model with matrices: \[ \boxed{\begin{bmatrix}\text{PERF}_i\\\text{USE}_i\end{bmatrix} =\begin{bmatrix}1&0\\0&1\end{bmatrix}\begin{bmatrix}\beta_{0,\text{PERF}}\\\beta_{0,\text{USE}}\end{bmatrix} + \begin{bmatrix}e_{i,\text{PERF}}\\e_{i,\text{USE}}\end{bmatrix}} \]

\[ \boxed{\mathbf{Y_i = X_iB + e_i}} \]

• Using expected values and linear combination rules, we can show that:

\[ \boxed{\begin{bmatrix}\text{PERF}_i\\\text{USE}_i\end{bmatrix} \sim \mathbf{N}_2 (\boldsymbol{\mu}_i=\begin{bmatrix}\beta_{0,\text{PERF}}\\\beta_{0,\text{USE}}\end{bmatrix}, \mathbf{V}_i =\mathbf{R}=\begin{bmatrix}\sigma^2_{e,\text{PERF}} & \sigma_{e,\text{PERF},\text{USE}}\\ \sigma_{e,\text{PERF},\text{USE}}&\sigma^2_{e,\text{USE}}\end{bmatrix})} \]

\[ \boxed{\mathbf{Y}_i \sim N_2(\mathbf{X}_i\mathbf{B},\mathbf{V}_i)} \]

Model 2: Multivariate Empty Model

Aim: To untangle the simple correlation between perf and use . We call it “empty”, because no predictor is used to explain the variances of the two variables.

Parameters: Number of parameters is 5, including two variables’ means and three variance-and-covaraince components.

model02.syntax = "
# Variances:
1perf ~~ perf
2use ~~ use

# Covariance:
3perf ~~ use

# Means:
4perf ~ 1
5use ~ 1
"

1

\(\sigma^2_{e, \text{PERF}}\)

2

\(\sigma^2_{e,\text{USE}}\)

3

\(\sigma^2_{e, \text{PERF}, \text{USE}}\)

4

\(\beta_{0, \text{PERF}}\)

5

\(\beta_{0, \text{USE}}\)

Properties of this model:

• This model is said to be saturated: All parameters are estimated - It is also called an unstructured covariance matrix

• No other structure for the covariance matrix can fit better (only as well as)

• The model for the means are two simple regression models without any predictors

Multivariate Correlation Model Results

Output of lavaan

## Estimation for model01
model02.fit <- cfa(model02.syntax, data=dataMath, mimic="MPLUS", fixed.x = TRUE, estimator = "MLR") 

## Print output
summary(model02.fit)

lavaan 0.6-19 ended normally after 29 iterations

  Estimator                                         ML
  Optimization method                           NLMINB
  Number of model parameters                         5

                                                  Used       Total
  Number of observations                           348         350
  Number of missing patterns                         3            

Model Test User Model:
                                              Standard      Scaled
  Test Statistic                                 0.000       0.000
  Degrees of freedom                                 0           0

Parameter Estimates:

  Standard errors                             Sandwich
  Information bread                           Observed
  Observed information based on                Hessian

Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)
  perf ~~                                             
    use               6.847    2.850    2.403    0.016

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)
    perf             13.959    0.174   80.442    0.000
    use              52.440    0.872   60.140    0.000

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)
    perf              8.742    0.754   11.596    0.000
    use             249.245   19.212   12.973    0.000

Question: why is the sample size different from Model 1?

By default, lavaan::cfa() use the listwise deletion. In Model 1, cases with non-NA values of perf are left. In Model 2, cases with both non-NA in perf and non-NA in use are left.

table(is.na(dataMath$perf))

FALSE  TRUE 
  290    60 

table(is.na(dataMath$perf) & is.na(dataMath$use))

FALSE  TRUE 
  348     2 

Correlation Between PERF and USE

# Covaraince Estimates
parameterestimates(model02.fit)[1:3,] |> show_table()

lhs	op	rhs	est	se	z	pvalue	ci.lower	ci.upper
perf	~~	perf	8.74	0.754	11.6	0.000	7.26	10.2
use	~~	use	249.25	19.212	13.0	0.000	211.59	286.9
perf	~~	use	6.85	2.850	2.4	0.016	1.26	12.4

# Standardized Parameters
standardizedsolution(model02.fit)[1:3,] |> show_table()

lhs	op	rhs	est.std	se	z	pvalue	ci.lower	ci.upper
perf	~~	perf	1.000	0.00	NA	NA	1.000	1.000
use	~~	use	1.000	0.00	NA	NA	1.000	1.000
perf	~~	use	0.147	0.06	2.44	0.015	0.029	0.265

D = matrix(c(sqrt(8.742), 0, 0,  sqrt(249.245)), nrow = 2)
S = matrix(c(8.742, 6.847, 6.847,  249.245), nrow = 2)
solve(D) %*% S %*% solve(D)

      [,1]  [,2]
[1,] 1.000 0.147
[2,] 0.147 1.000

• Result: The students’ math performance are significantly correlated with their perceived usefulness of math (r = .147, p = .016), but the correlation coefficient is weak.

Comparing Model with Data

library(mvtnorm)
x = expand.grid(
  perf = seq(0, 25, .1),
  use = seq(0, 120, .1)
)
sim_dat <- cbind(
  x,
  density = dmvnorm(x, mean = c(13.959, 52.440), sigma = S)
)

  
mod2_density <- ggplot() +
  geom_contour_filled(aes(x = perf, y = use, z = density), data = sim_dat) +
  geom_point(aes(x = perf, y = use), data = dataMath, colour = "white", alpha = .5) +
  labs( x= "PERF", y="USE") +
  theme_classic() +
  theme(text = element_text(size = 20)) 
mod2_density

• We can use our estimated parameters to simulation the model-implied density plot for perf and use, which can be compared to the observed data of perf and use

Interactive 3D Plot for Estimated MVN

\[ \begin{bmatrix}\text{PERF}_i\\\text{USE}_i\end{bmatrix} \sim \mathbf{N}_2 (\boldsymbol{\mu}_i=\begin{bmatrix}13.959\\52.440\end{bmatrix}, \mathbf{V}_i =\mathbf{R}=\begin{bmatrix}8.742 & 6.847\\ 6.847 & 249.245 \end{bmatrix}) \]

library(plotly)
density_surface <- sim_dat |> 
  pivot_wider(names_from = use, values_from = density) |> 
  select(-perf) |> 
  as.matrix()
plot_ly(z = density_surface, x = seq(0, 120, .1), y = seq(0, 25, .1), colors = "PuRd", color = "green",
        width = 1600, height = 800) |> add_surface() 

Multivariate Regression Model Estimated Density

A Different Model for the data

• To demonstrate how models may vary in terms of model fit (and to set up a discussion of model fit and model comparisons) we will estimate a model where we set the covariance between PERF and USE to zero.
  • Zero covariance implies zero correlation – which is unlikely to be true given our previous analysis
• You likely would not use this model in a real data analysis
  • If anything, you may start with a zero covariance and then estimate one
• But, this will help to introduce come concepts needed to assess the quality of the multivariate model

Model 3: Multivariate Empty Model with Zero Covariance

One way to double check whether the “correlation” is important is to deliberately fix the “correlation” to be 0 and then compare this model to the previous model to see if it get much worse.

model03.syntax = "
# Variances:
perf ~~ perf 
use ~~ use   

# Covariance:
1perf ~~ 0*use

# Means:
perf ~ 1  
use ~ 1   
"

1

We constrain the residual covaraince between perf and use \(\sigma_{e, \text{PERF}, \text{USE}} = 0\) using 0*

## Estimation for model01
model03.fit <- cfa(model03.syntax, data=dataMath, mimic="MPLUS", fixed.x = TRUE, estimator = "MLR") 

## Print output
parameterestimates(model03.fit) |> show_table()

lhs	op	rhs	est	se	z	pvalue	ci.lower	ci.upper
perf	~~	perf	8.75	0.756	11.6	0	7.27	10.2
use	~~	use	249.20	19.212	13.0	0	211.55	286.9
perf	~~	use	0.00	0.000	NA	NA	0.00	0.0
perf	~1		13.97	0.174	80.4	0	13.62	14.3
use	~1		52.50	0.874	60.0	0	50.79	54.2

Model Assumption

• The zero covariance now leads to the following assumptions about the data:

  \[ \begin{bmatrix}\text{PERF}_i\\\text{USE}_i\end{bmatrix} \sim \mathbf{N}_2 (\boldsymbol{\mu}_i=\begin{bmatrix}13.959\\52.440\end{bmatrix}, \mathbf{V}_i =\mathbf{R}=\begin{bmatrix} 8.750 & \color{tomato}{0} \\ \color{tomato}{0} & 249.200 \end{bmatrix}) \]

• Because these are MVN, we are assuming PERF is independent from USE (they have zero correlation/covariance)

Question

Our new model (zero covariance) is better or worse fitting to data compared to our previous model (freely estimated covariance)?

Answer

I think Model 3 is worse because of fewer parameters and stronger assumptions. We don’t know yet the degree of “worse” is significant or not.

anova(model02.fit, model03.fit)

Scaled Chi-Squared Difference Test (method = "satorra.bentler.2001")

lavaan->lavTestLRT():  
   lavaan NOTE: The "Chisq" column contains standard test statistics, not the 
   robust test that should be reported per model. A robust difference test is 
   a function of two standard (not robust) statistics.
            Df  AIC  BIC Chisq Chisq diff Df diff Pr(>Chisq)  
model02.fit  0 4180 4199  0.00                                
model03.fit  1 4184 4200  6.06       5.57       1      0.018 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Model Results

parameterestimates(model02.fit) |> show_table()

lhs	op	rhs	est	se	z	pvalue	ci.lower	ci.upper
perf	~~	perf	8.74	0.754	11.6	0.000	7.26	10.2
use	~~	use	249.25	19.212	13.0	0.000	211.59	286.9
perf	~~	use	6.85	2.850	2.4	0.016	1.26	12.4
perf	~1		13.96	0.174	80.4	0.000	13.62	14.3
use	~1		52.44	0.872	60.1	0.000	50.73	54.1

parameterestimates(model03.fit) |> show_table()

lhs	op	rhs	est	se	z	pvalue	ci.lower	ci.upper
perf	~~	perf	8.75	0.756	11.6	0	7.27	10.2
use	~~	use	249.20	19.212	13.0	0	211.55	286.9
perf	~~	use	0.00	0.000	NA	NA	0.00	0.0
perf	~1		13.97	0.174	80.4	0	13.62	14.3
use	~1		52.50	0.874	60.0	0	50.79	54.2

Examining Model/Data Fit

sim_dat_2 <- cbind(
  x,
  density = dmvnorm(x, mean = c(13.959, 52.440), 
                    sigma = matrix(c(8.750535, 0, 0, 249.200921), nrow = 2))
)

  
mod3_density <- ggplot() +
  geom_contour_filled(aes(x = perf, y = use, z = density), data = sim_dat_2) +
  geom_point(aes(x = perf, y = use), data = dataMath, colour = "white", alpha = .5) +
  labs( x= "PERF", y="USE", title = "Model 3's Density") +
  theme_classic() +
  theme(text = element_text(size = 20)) 

mod2_density

mod3_density

Homework 2

1. Use lavaan and dataMath to test the correlations among Math Performance (perf), Math Anxiety (mas), and Perceived Usefulness of Mathematics (use).

   • Model 1: All correlations are freely estimated.
     • Q1/Q2/Q3: What are the estimated correlations/SD/p.values for Performance - Anxiety, Performance - Usefulness, and Anxiety - Usefulness, respectively (the results should have two-digit precision).
     • Q4: What are AIC and BIC for Model 1 (one-digit precision)
   • Model 2: Fix the correlation between math anxiety (mas) and perceived usefulness of mathematics (use) to 0; Leave the other correlations to be freely estimated.
     • Q5/Q6/Q7: What are the estimated correlations/SD/p.values for Performance - Anxiety, Performance - Usefulness, and Anxiety - Usefulness, respectively (the results should have two-digit precision)..
     • Q8: What are AIC and BIC for Mode 2 (one-digit precision)
   • Q9: Provide the evidence of significance testing for the model comparison between Model 1 and Model 2. Write down your conclusion about which model is better and whether the difference is significant.
   • Q10: Copy and paste your R syntax (make sure you use lavaan syntax)
   Scoring Details (Total Points: 21)

   • Two points: Q1, Q2, Q3, Q5, Q6, Q7; (12 points total)

   • Three points: Q4, Q5, Q9; (9 points total)

   • Q10 (bonus: extra 3 points)

Wrapping Up

1. This lecture was an introduction to the estimation of multivariate linear models for multivariate outcomes the using path analysis/SEM package lavaan

2. We saw that the model for continuous data uses the multivariate normal distribution in its likelihood function

Next Class

1. Does each model fit the data well (absolute model fit)?
2. If not, how can we improve model fit?
3. Which model fits better (relative model fit)?
4. Answers are given in the following lectures…